Angular Temperature Distribution in a Solar Receiver Tube
What is The Project?
The following is a project I completed within my heat transfer course. The project consists of a two part analysis of the temperature distribution for a tube bank that acts as a solar thermal receiver.
Problem Statement
Supercritical water flowing through the tubes gets heated by the solar radiation incident on the tubes. The tubes are made of ceramic and have a thermal conductivity of 80 W/m-K. The tubes have an inner radius of 15 mm, and their wall thickness is 3 mm. The outer diameter of the tube has a thin layer of coating whose absorptivity to solar radiation is 0.95. The contact resistance between the coating and the outer diameter of the tube is 𝑅𝑡,𝑐 = 10^-4 𝑚 − 𝑘/𝑊. The amount of solar radiation incident normal to the tube surface depends on the angle to the concentrated solar flux and is given as Q = Qo cos (θ). The range of θ varies from -90 to 90 degrees. The value of q is 100*104 W/m2. On a regular summer day, the ambient air temperature is 40C, and the heat transfer coefficient between the tube and air is 25 W/m2-K. At steady-state, the supercritical water inside the tubes gets heated to a temperature of 600C. The convective heat transfer coefficient between the tube and supercritical water is 1000 W/m2-K.
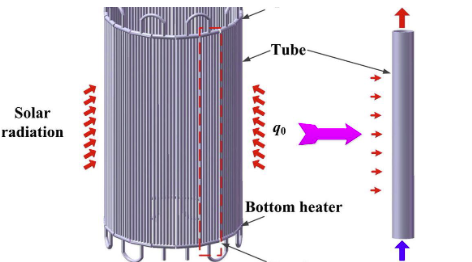

Part A: Steady-State Temperature Distribution
First I must find the steady-state temperature distribution of the tube walls in the angular direction. I neglected radial temperature variation within the tube and emission in my calculation.
Calculations:
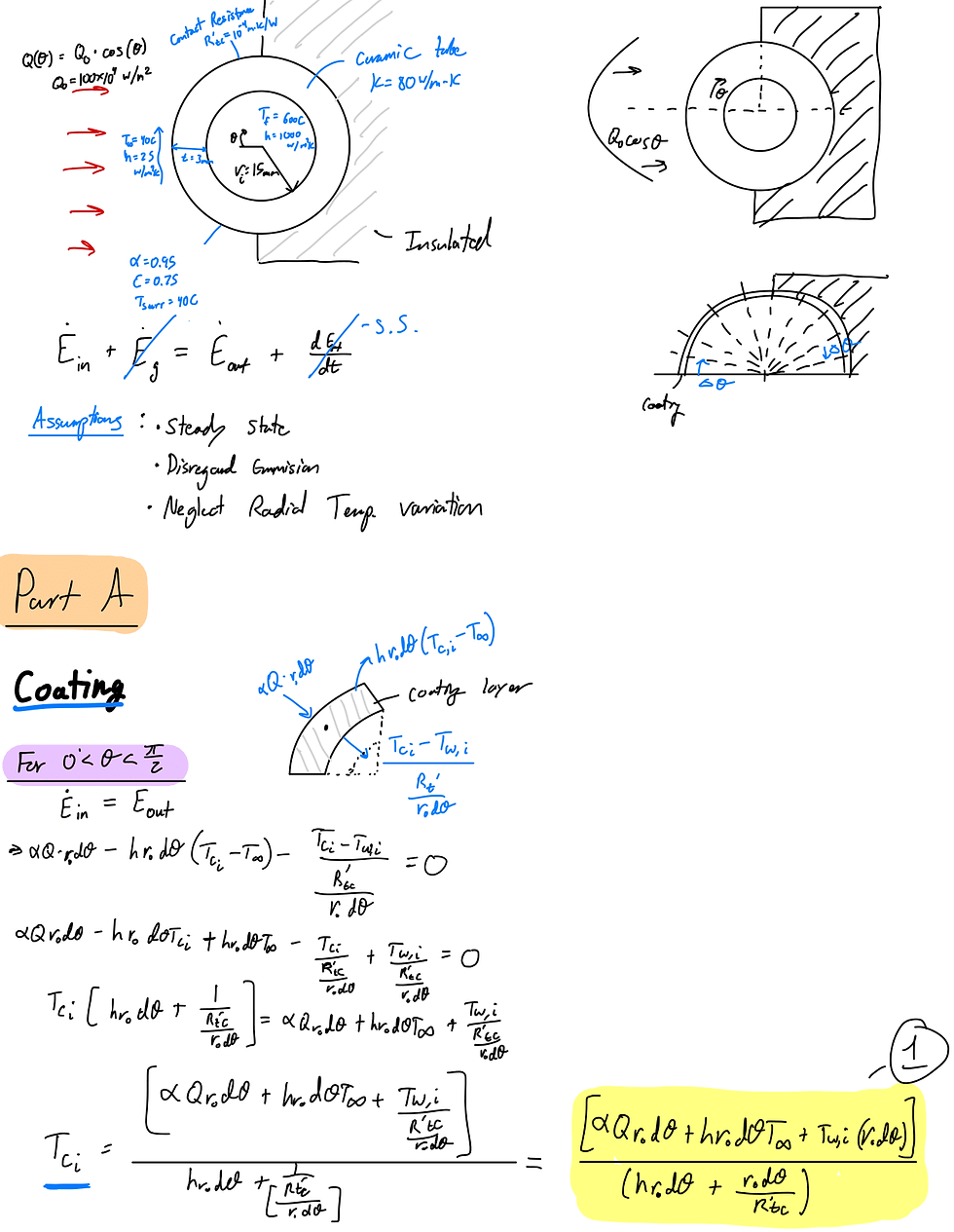
Describe your image

Describe your image

Describe your image

Describe your image
MATLAB Script
Having found my equations, I set up a MATLAB script to solve and plot the temperature distribution of the tube bank. Below is the MATLAB script I created for solving the first part of this problem.

Describe your image
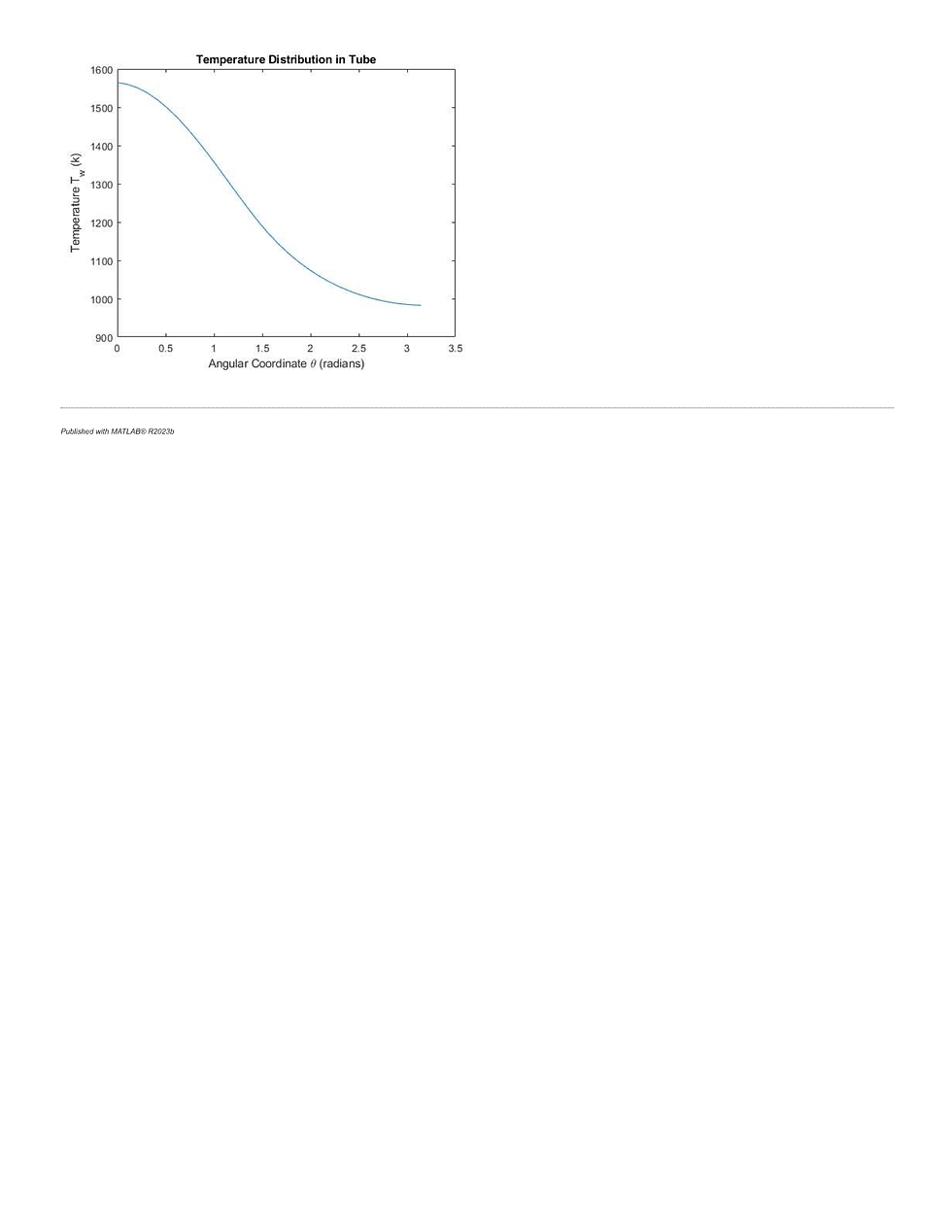
Describe your image

Describe your image
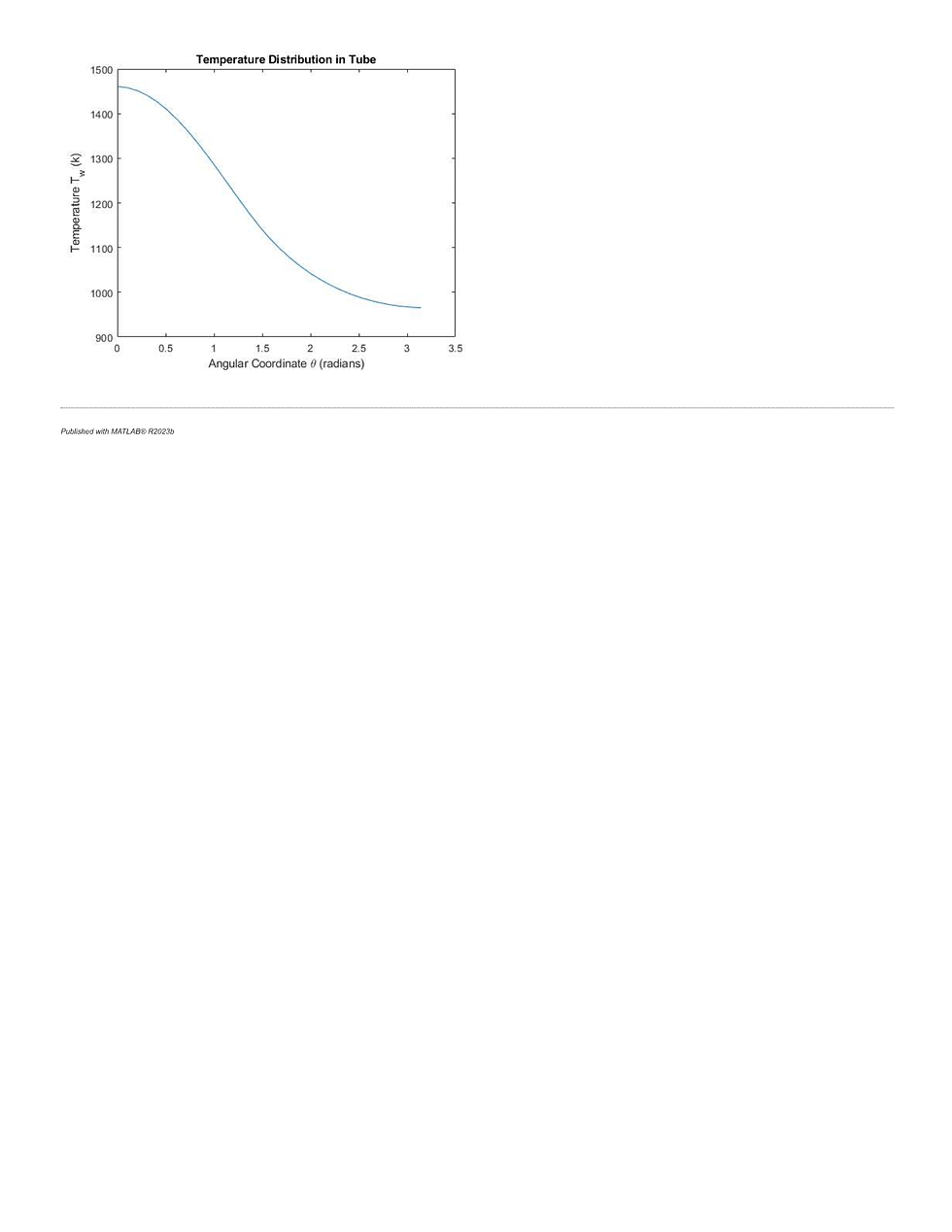
Part B: Steady-State Temperature Distribution With Emission
I found the steady-state temperature distribution of the tube walls in the angular direction with the effect of emission in my calculations. The coating has an emissivity of 0.75 to long wave radiation and the surrounding temperature is 40C.
Calculations:
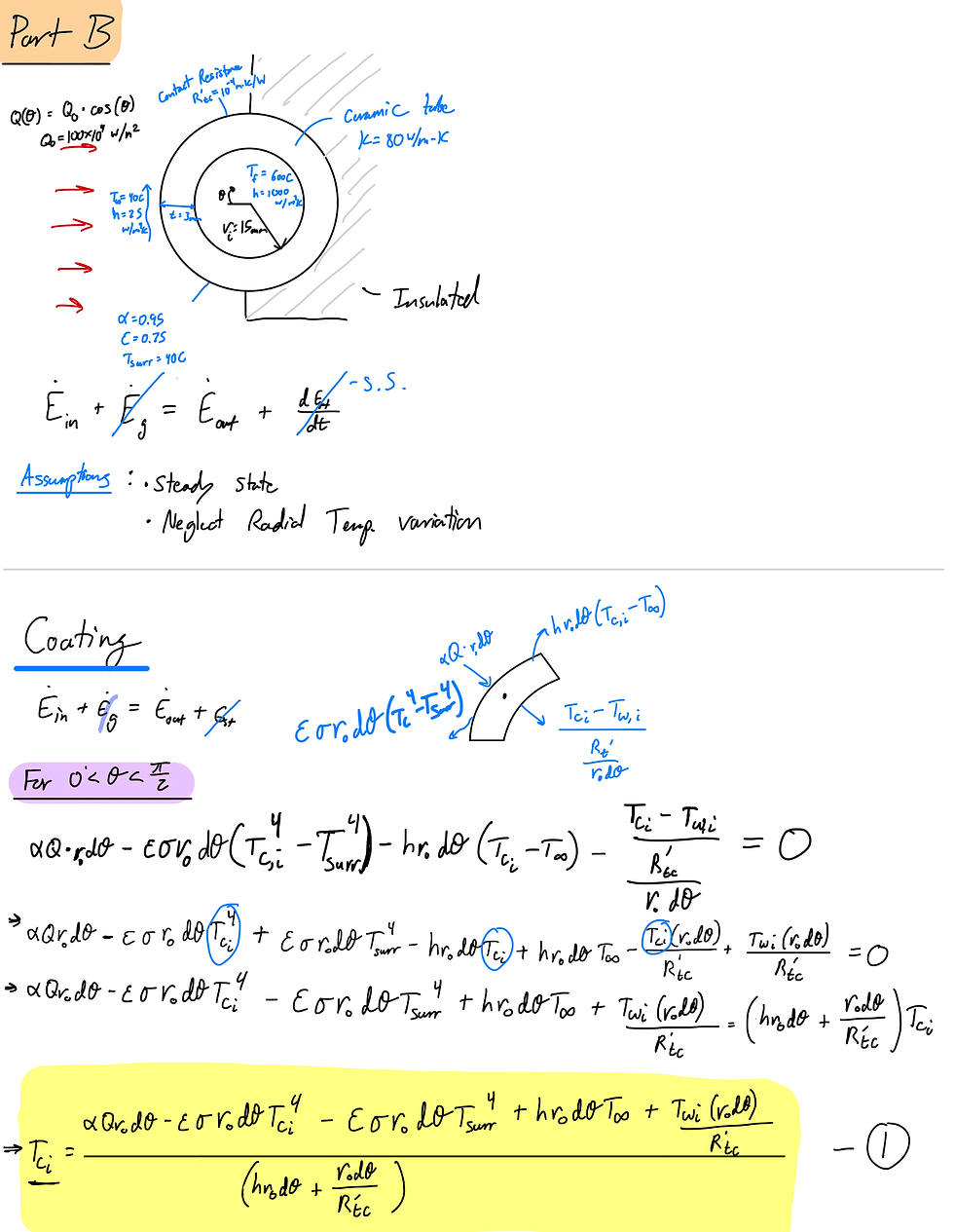
Describe your image

Describe your image

Describe your image

Describe your image
MATLAB Script
Having found my equations, I set up a MATLAB script to solve and plot the temperature distribution of the tube bank. Below is the MATLAB script I created for solving the second part of this problem.

Describe your image
Describe your image

Describe your image
Comparison
Taking into account emission causes there to be a decrease in the temperature of the walls. Heat in the system is lost due to radiation. We can see this in the results of part b, which has a max wall temperature that is ~100K lower than our tube in part a.